Moserville

Lemma 7½

For any convex shape $C$, the diameter of any element of $[C,G]^-$ is $\text{max}\left(\text{diam}\left(G\right), \text{diam}\left(C\right)\right)$.

proof:

First, if $\text{diam}\left(C\right) \geq 1$, then $G$ is accomodated by $C$, meaning that any element of $[C,G]^-$ is $C$, and so has a diameter of $\text{diam}\left(C\right)$. Therefore, assume $\text{diam}\left(C\right) < 1$

Let $c$ and $g$ be instances of $C$ and $G$, and suppose $\text{diam}([c,g])>1$. Because the convex hull of a shape has the same diameter as the shape itself, there are two points in $c\cup g$ that lie more than a unit apart. Neither $c$ nor $g$ has a diameter above 1, so one of these points must lie outside $c$, and one lies outside $p$. Therefore, define $p_c\in c/g$ and $p_g\in g/c$, with $\ell\left\langle p_c,p_g\right\rangle > 1$. There exists a pair of points on $\left\langle p_c, p_g\right\rangle$ that are a unit apart, one of which is internal to $c$. By Corrolary 4½.1, $c$ and $g$ are not fully intersecting, and so $[c,g]\not\in[C,G]^-$ by Theorem 4.

$\square$

This is a milder version of a much more significant theorem that this section has been building to.

Theorem 4¾

For any convex shapes $C$ and $D$, the diameter of any element of $[C,D]^-$ is $\text{max}\left(\text{diam}\left(C\right), \text{diam}\left(D\right)\right)$.

proof:

Without loss of generality, assume $\text{diam}\left(C\right) \geq \text{diam}\left(D\right)$. To force a contradiction, assume $[c,d]\in[C,D]^-$ where $\text{diam}\left([c,d]\right) > \text{diam}\left(C\right)$. Additionally, without loss of generality, we may imagine zooming in or out until

$$\text{diam}\left(C\right) = 1 \geq \text{diam}\left(D\right)$$

Next, without loss of generality, imagine rotating and translating $[c,d]$ such that the two points in $c$ with a distance of 1 unit lie on $\left(0,0\right)$ and $\left(1,0\right)$. Define $c_t$ to be the boundary of $c$ that lies above the $x$-axis, and define $c_b$ to be the boundary of $c$ that lies below the $x$-axis. Because $\text{diam}\left([c,d]\right) > 1$, there exists a point on the boundary of $c/d$, and a point on the boundary of $d/c$ that are more than a unit apart. Therefore, define $p_c\in c$ and $p_d\in d$ to be two points such that

$$\ell\left\langle p_c,p_d\right\rangle >1$$

As of right now, $c$ only has points defined at $\left(0,0\right)$ and $\left(1,0\right)$, and so this setup is symmetric around the $x$-axis and $x=0.5$. Therefore, assume without loss of generality that $p_d$ has a $y$ coordinate greater than or equal to 0, and a $x$ coordinate greater than or equal to 0.5. If $p_c$ lies on $c_t$, there is a point on $c_b$ that is even further from $p_d$, so assume $p_c$ lies on $c_b$. In total, the situation looks like this:

Unfortunately, I don’t think we can make any more assumptions without loss of generality from here. One thing we do know is that $d$ must be fully intersecting with $c$, and therefore must “cross” through it. There is therefore a line inside $d$ that passes from one boundary point of $c$ to another. This line can either pass from $c_t$ to $c_b$, or it doesn’t, in which case the line must pass through $c_t$ twice. These two possibilities are illustrated below:

Case 1	Case 2

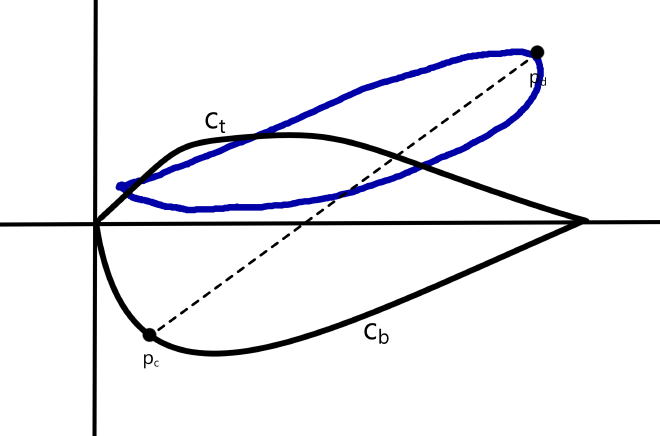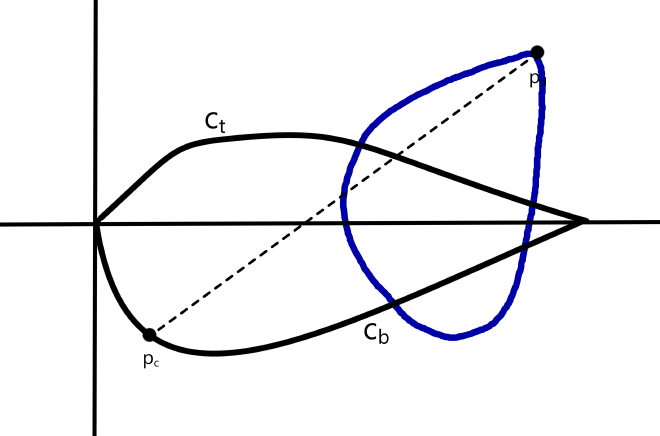For now, let’s assume Case 1, so that there is no line in $d$ passing through $c_b$, but there is a line that passes through $c_t$ twice.

Let $d_1$ be the point in $d$ with the lowest $x$ coordinate, and let $d_2$ be the point in $d$ with the greatest $x$ coordinate.

$\square$